For some Maths can be fun and for some, it can be a nightmare. Maths Formulas are difficult to memorize and we have curated a list of Maths Formulas for Class 12 PDF State Board just for you. You can use this as a go-to sheet whenever you want to prepare Class 12 Maths Formulas. Students can get Formulas in Algebra, Calculus, and Geometry that can be useful in their preparation and help them do their homework.
Here in this article Maths Formulas for Class 12 PDF State Board, we have listed basic Maths formulas so that you can learn the fundamentals of Maths. Our unique way of solving Maths Problems will make you learn how the equation came into existence instead of memorizing it. Solve all the important problems and questions in Maths with the Best Maths Formulas for Class 12.
Maths Formulas for Class 12 PDF State Board
Feel free to directly use the best Maths formulas during your homework or exam preparation. You need to know the list of Class 12 formulas as they will not just be useful in your academic books but also in your day-to-day lives.
Remember the Maths Formulas smartly by making use of our list. You can practice Questions and Answers based on these Class 12 Maths Formulas. Students can get basic Maths formulas Free PDF Download for Class 12. Candidates can use the handy learning aid Maths Formulas PDF to have in-depth knowledge on the subject as per the latest CBSE Syllabus.
CBSE Class 12 Maths Formulas according to the Chapters are prepared by subject experts and you can rely on them during your preparation. Click on the topic you wish to prepare from the list of formulas prevailing.
Download the 12th Maths Formulas List Pdf State Board below:
Name 12th Maths Formulas List Pdf State Board.
Format: PDF
Size: 1 MB
>> Maths Formulas for Class 12 PDF State Board Chapter Wise <<
File Link: Download Here
Alternate Server: 12th Maths Formulas List Pdf State Board
12th Maths Formulas List
Areas
| Square |  | A=l2 | l : length of side |
| Rectangle |  | A=w×h | w : width h : height |
| Triangle | 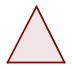 | A=b×h2 | b : base h : height |
| Rhombus |  | A=D×d2 | D : large diagonal d : small diagonal |
| Trapezoid |  | A=B+b2×h | B : large side b : small side h: height |
| Regular polygon |  | A=P2×a | P : perimeter a : apothem |
| Circle |  | A=πr2 P=2πr | r : radius P : perimeter |
| Cone (lateral surface) |  | A=πr×s | r : radius s : slant height |
| Sphere (surface area) |  | A=4πr2 | r: radius |
Volumes
| Cube |  | V=s3V=s3 | ss: side |
| Parallelepiped |  | V=l×w×hV=l×w×h | ll: length ww: width hh: height |
| Regular prism |  | V=b×hV=b×h | bb: base hh: height |
| Cylinder |  | V=πr2×hV=πr2×h | rr: radius hh: height |
| Cone (or pyramid) |  | V=13b×hV=13b×h | bb: base hh: height |
| Sphere |  | V=43πr3V=43πr3 | rr: radius |
Functions and Equations
| Directly Proportional | y=kxy=kx k=yxk=yx | kk: Constant of Proportionality |
| Inversely Proportional | y=kxy=kx k=yxk=yx | |
| ax2+bx+c=0ax2+bx+c=0 | Quadratic formula | x=−b±b2−4ac−−−−−−−√2ax=-b±b2-4ac2a |
| Concavity | Concave up: a>0a>0 | |
| Concave down: a<0a<0 | ||
| Discriminant | Δ=b2−4acΔ=b2-4ac | |
| Vertex of the parabola | V(−b2a,−Δ4a)V(-b2a,-Δ4a) | |
| y=a(x−h)2+ky=a(x-h)2+k | Concavity | Concave up: a>0a>0 |
| Concave down: a<0a<0 | ||
| Vertex of the parabola | V(h,k)V(h,k) | |
| Zero-product property | A×B=0⇔A=0∨B=0A×B=0⇔A=0∨B=0 | ex : (x+2)×(x−1)=0⇔(x+2)×(x-1)=0⇔ x+2=0∨x−1=0⇔x=−2∨x=1x+2=0∨x-1=0⇔x=-2∨x=1 |
| Difference of two squares | (a−b)(a+b)=a2−b2(a-b)(a+b)=a2-b2 | ex : (x−2)(x+2)=x2−22=x2−4(x-2)(x+2)=x2-22=x2-4 |
| Perfect square trinomial | (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2 | ex : (2x+3)2=(2x)2+2⋅2x⋅3+32=(2x+3)2=(2x)2+2⋅2x⋅3+32= 4×2+12x+94×2+12x+9 |
| Binomial theorem | (x+y)n=∑k=0nnCkxn−kyk |
Probability and Sets
| Commutative | A∪B=B∪AA∪B=B∪A | A∩B=B∩AA∩B=B∩A |
| Associative | A∪(B∪C)=A∪(B∪C)A∪(B∪C)=A∪(B∪C) | A∩(B∩C)=A∩(B∩C)A∩(B∩C)=A∩(B∩C) |
| Neutral element | A∪∅=AA∪∅=A | A∩E=AA∩E=A |
| Absorbing element | A∪E=EA∪E=E | A∩∅=∅A∩∅=∅ |
| Distributive | A∪(B∩C)=(A∪B)∩(A∪C)A∪(B∩C)=(A∪B)∩(A∪C) | A∩(B∪C)=(A∩B)∪(A∩C)A∩(B∪C)=(A∩B)∪(A∩C) |
| De Morgan’s laws | A∩B¯¯¯¯¯¯¯¯¯=A¯¯¯∪B¯¯¯A∩B¯=A¯∪B¯ | A∪B¯¯¯¯¯¯¯¯¯=A¯¯¯∩B¯¯¯A∪B¯=A¯∩B¯ |
| Laplace laws | P(A)=Number of ways it can happen Total number of outcomes P(A)=Number of ways it can happen Total number of outcomes | |
| Complement of an Event | P(A¯¯¯)=1−P(A)P(A¯)=1-P(A) | |
| Union of Events | P(A∪B)=P(A)+P(B)−P(A∩B)P(A∪B)=P(A)+P(B)-P(A∩B) | |
| Conditional Probability | P(A∣B)=P(A∩B)P(B)P(A∣B)=P(A∩B)P(B) | |
| Independent Events | P(A∣B)=P(A)P(A∣B)=P(A) | P(A∩B)=P(A)×P(B)P(A∩B)=P(A)×P(B) |
| Permutation | Pn=n!=n×(n−1)×…×2×1Pn=n!=n×(n-1)×…×2×1 | ex : P4=4!=4×3×2×1=24P4=4!=4×3×2×1=24 |
| Permutations without repetition | nAp=n!(n−p)!nAp=n!(n-p)! | ex : 6A2=6!(6−2)!=306A2=6!(6-2)!=30 |
| Permutations with repetition | nA′p=npnAp′=np | ex : 5A′3=53=1255A3′=53=125 |
| Combination | nCp=nApp!=n!(n−p)!×p!nCp=nApp!=n!(n-p)!×p! | ex : 5C4=5A44!=55C4=5A44!=5 |
| Probability Distribution | Average value | μ=x1p1+x2p2+…+xkpkμ=x1p1+x2p2+…+xkpk |
| Standard deviation | σ=∑i=1kpi(xi−μ)2−−−−−−−−−−−−⎷σ=∑i=1kpi(xi-μ)2 | |
| Binomial distribution | P(X=k)=nCk.pk.(1−p)n−kP(X=k)=nCk.pk.(1-p)n-k | ex : B(10;0,6)B(10;0,6) P(X=3)=10C3×0,63×0,47P(X=3)=10C3×0,63×0,47 |
Enjoy our other study material free of cost for your examination, also share this with your friends.
If you liked this article and got to learn something, then please share this post on social networks such as Facebook, Twitter, and other social media sites.
This is a great post. I am a student of Class 12 and I am finding it difficult to remember all the formulas. This post has helped me a lot.
Great resource for class 12 maths formulas! Helped me revise for my state board exams with ease. Thanks for sharing!
Thank you for providing this comprehensive PDF of Maths formulas for Class 12! It’s so helpful to have all the essential formulas in one place for quick reference. I’m sure it will make studying a lot easier for all of us preparing for the exams. Great job!